复杂加法器的旅程从单个比特的加法开始:此时不考虑进位CARRY,只看求和SUM
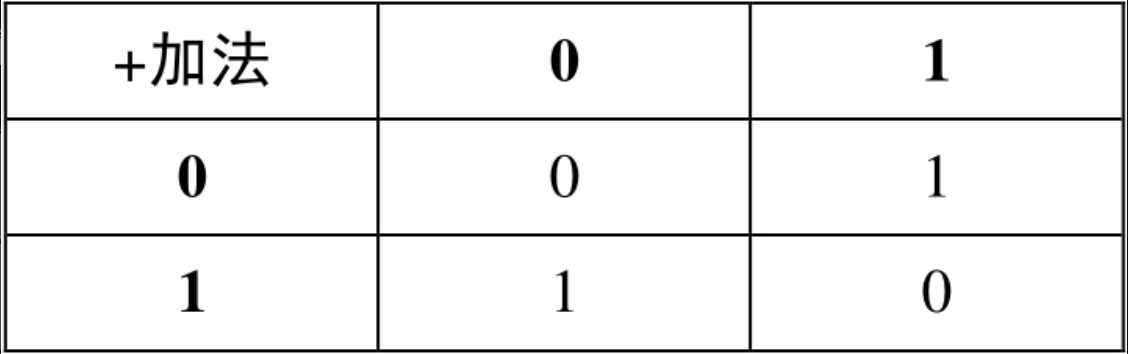
求SUM的结果有点像或门OR,但除了右下角的值
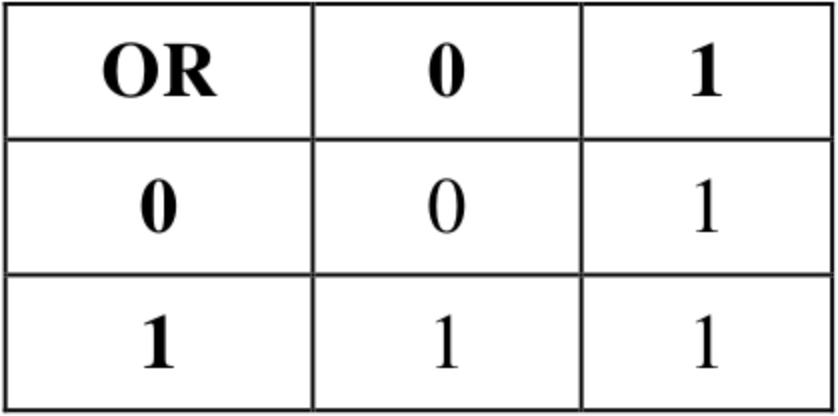
求SUM的结果有点像与非门NAND,但除了左上角的值
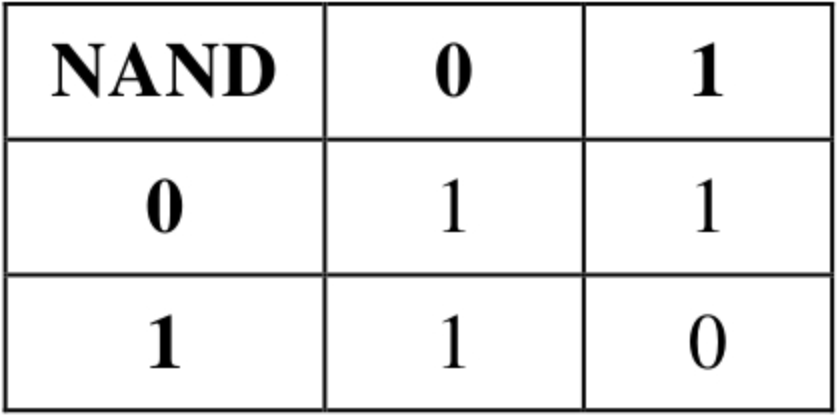
这样的话,能不能把两者结合一下呢
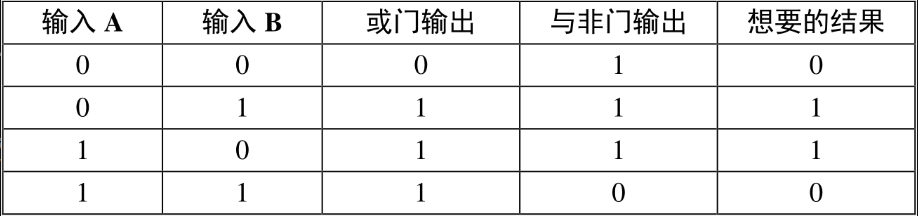
注意,我们想要的是1,那么这种情况只有在或门和与非门的输出都为1时才会出现。
这表明或门、与非门输出端可以通过一个与门连接到一起。
可点击下图左侧的数字输入框,然后查看SUM的结果
此部分对应第一版原文《第12章 二进制加法器》
建议结合原文进行交互阅读
加法计算就是计算机要做的唯一工作。
如果我们可以造出加法器,同样地,就可以利用加法来实现减法、乘法和除法
计算按揭付款,引导火箭飞到火星、下棋,以及填写我们的话费账单
在这些电路中,您可以通过点击方形按钮来选择要相加的数字。
这些按钮可以通过鼠标点击或手指触摸来切换,输出结果将显示在圆圈中。
这些动画中的所有门电路的传播时间都设置为100毫秒(1/10秒)。
当您切换其中一个开关时,可以看到比特从左向右传播。
如果你对简化后逻辑门符号感到陌生🤔,建议回看 继电器与逻辑门这一部分内容
复杂加法器的旅程从单个比特的加法开始:此时不考虑进位CARRY,只看求和SUM

求SUM的结果有点像或门OR,但除了右下角的值

求SUM的结果有点像与非门NAND,但除了左上角的值

这样的话,能不能把两者结合一下呢

注意,我们想要的是1,那么这种情况只有在或门和与非门的输出都为1时才会出现。
这表明或门、与非门输出端可以通过一个与门连接到一起。
可点击下图左侧的数字输入框,然后查看SUM的结果
在SUM一位加法器的基础上,现在补充一个进位CARRY输出位。
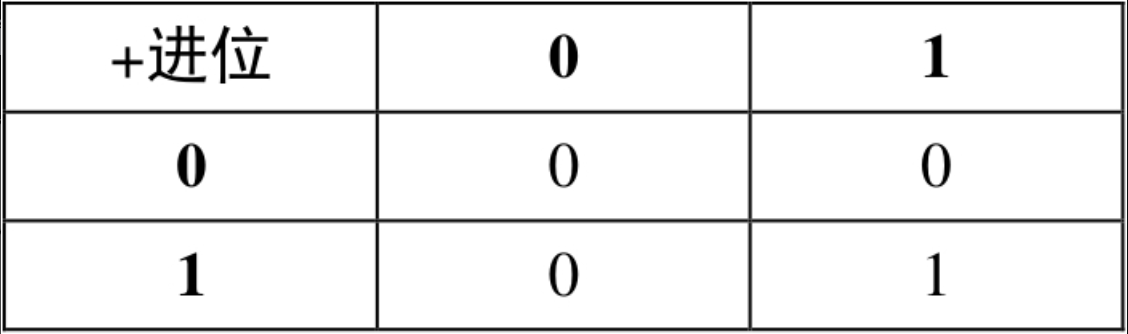
可见求进位CARRY的逻辑与AND逻辑门是一致的,因此我们就使用AND逻辑门
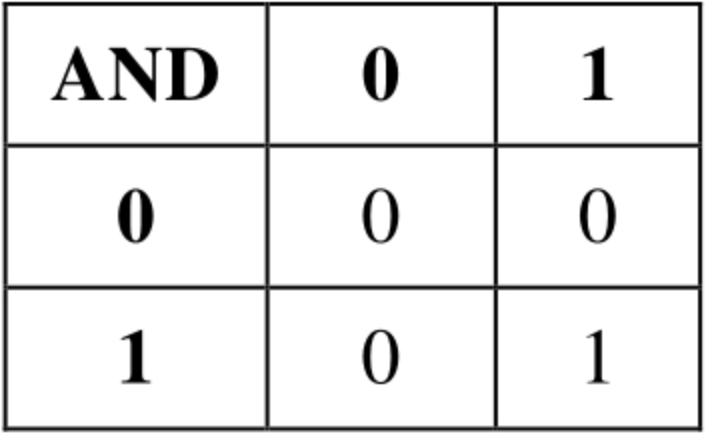
可点击下图左侧的数字输入框,然后查看SUM与CARRY的结果
上图的一位半加器的简易表示图如下

上方的加法器只能算是一个半加器
它将两个一位二进制数相加,得出一个加法位和一个进位位。
但是绝大多数二进制数是多于1位的。
半加器没有做到的是:将之前一次的加法可能产生的进位位纳入下一次运算
例如,假设我们要将如下两个二进制数相加。
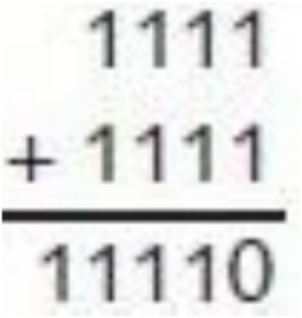
我们只能将半加器用于最右面一列的相加:1加1等于0,进位1。
对于从右面算起的第二列,由于进位位的存在,实际上需要将三个二进制数相加,而随后每一列的加法都是这样的。
前两列是两个加数,第三列是进位输入,第四列是加法结果,第五列是进位输出。
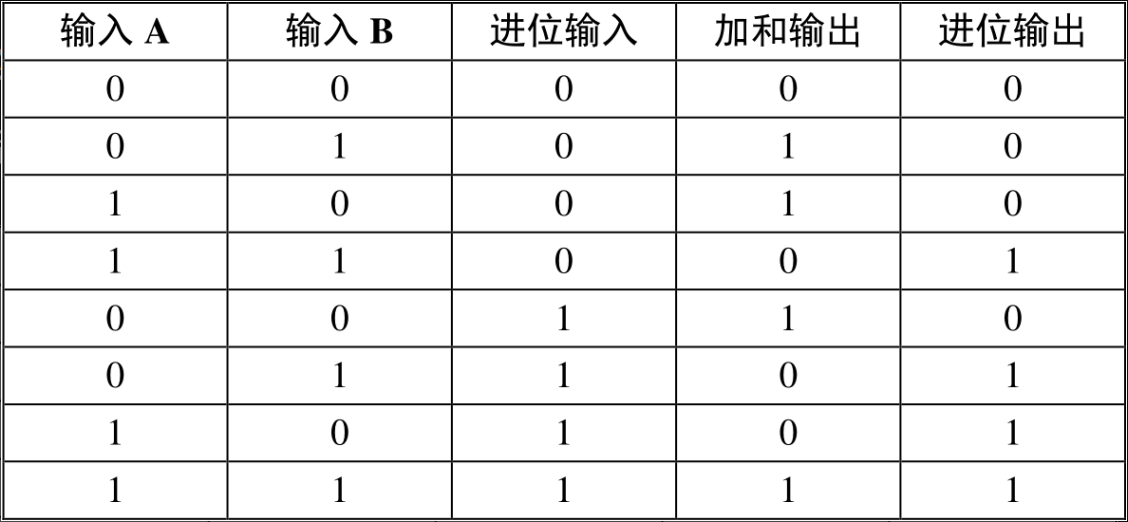
新增一个进位输入CARRY IN位后的电路图
全加器是由两个半加器加一个或门组合而来
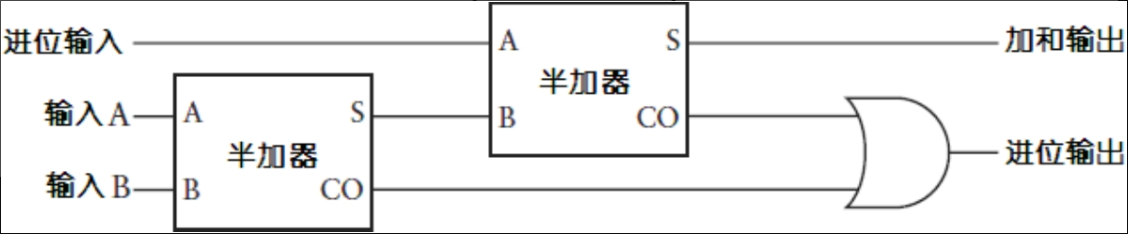
全加器的简化图如下,之后只会以简化图出现

最后,通过级联八个一位加法器可以相加整个字节。
通过点击或触摸顶部的方形按钮选择要相加的两个二进制值。
十六进制和十进制的值显示在最右侧。
二进制结果显示在底部的圆圈中
十六进制和十进制的等效值显示在最右侧。
(等于符号前面带h的是十六进制,后面不带h的是十进制)
每个加法器的进位输出 CARRY OUT都是下一个加法器的进位输入CARRY IN。
另外,如果想查看完整的传播延迟,尝试将整行顶部按钮设置为1,然后使用第二行的按钮加1。